
Project Euler #2: Even Fibonacci Numbers
The second problem on Project Euler is just as straightforward as the first one. In a nutshell, it asks us to find the sum of all even terms of the fibonacci sequence under 4 million. There is, however, one small modification - the numbers that we start with are 1 and 2 (instead of the usual 0 and 1).
The sequence we will be working with appears as follows:
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144....
The simplest solution is to just loop through each term of the sequence until we hit 4 million, and along the way, we keep summing up all the even numbers. It is the most obvious solution because we’re just following the instructions laid out by the question.
# start the fibonacci seq. with 1 and 2
a = 1
b = 2
# initialize 'sum' with 2
sum = 2
# calculate the current term and store it in 'c'
c = a + b
# run the loop as long as the current term is <= four million
while(c <= 4000000):
# make a = b, and b = c to advance through the sequence
a = b
b = c
# if the current term is an even number, add it to 'sum'
if not(c & 1):
sum += c
# calculate the next term of the fibonacci sequence
c = a + b
# print out the sum
print(sum)O(n), so not bad at all. However, there are some interesting observations to be made.
The very first observation to be made is to see if we can get the fibonacci spiral and the golden ratio from this series of numbers.
For those of you who are not aware of the golden ratio, it is a mathematical concept that has intrigued scholars and artists for centuries. It is often represented by the Greek letter phi (φ) and has a value of approximately 1.6180339887. This ratio has been found to appear in various natural and man-made phenomena, such as the proportions of the Parthenon in Athens, the growth patterns of sunflowers, and even in the human body.
When we take consecutive pairs of numbers in the Fibonacci sequence and calculate their ratios, we find that these ratios approach the value of the golden ratio as the terms in the sequence grow larger. In other words, if we divide a number in the Fibonacci sequence by its preceding number, the result will approximate the golden ratio. This relationship becomes more evident as we progress through the sequence. For example, 8 divided by 5 is equal to 1.6, while 21 divided by 13 equals approximately 1.615.
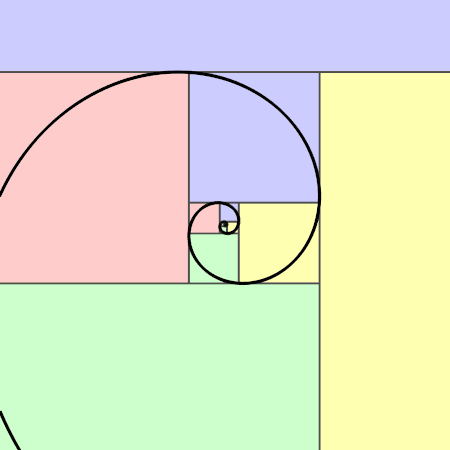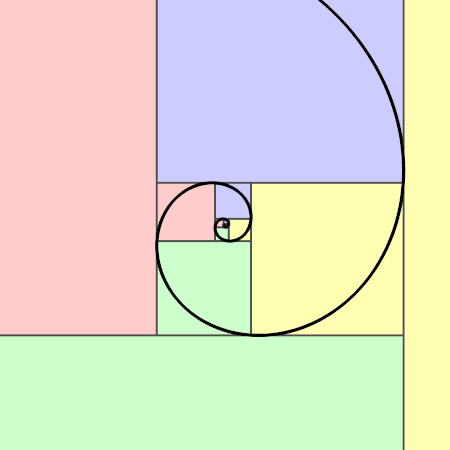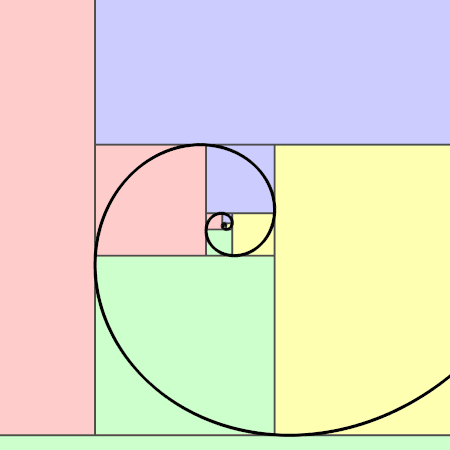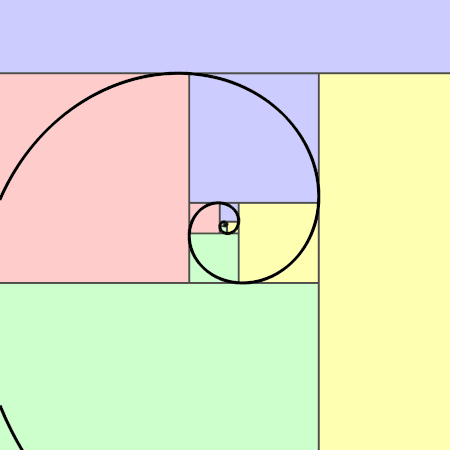
In our fibonacci sequence above, we can observe that the ratio of consecutive terms does indeed approach the golden ratio -
| a | b | Ratio (b/a) |
|---|---|---|
| 1 | 2 | 2 |
| 2 | 3 | 1.5 |
| 3 | 5 | 1.6667 |
| 5 | 8 | 1.6 |
| 8 | 13 | 1.625 |
| 13 | 21 | 1.6153 |
| 21 | 34 | 1.6190 |
| 34 | 55 | 1.6170 |
| 55 | 89 | 1.6181 |
| 89 | 144 | 1.618 |
Beyond ‘3’, every consequent fibonacci term can be obtained by multiplying the current term with the golden ratio and rounding it to the nearest integer.
So, in essence, we could re-factor our code to make it look like this:
# start the fibonacci seq. with 1 and 2
a = 1
b = 2
GOLDEN_RATIO = 1.6180339887
# initialize 'sum' with 2
sum = 2
# calculate the current term and store it in 'c'
c = a + b # here, it is 3
# run the loop as long as the current term is <= four million
while(c <= 4000000):
# calculate the next term of the fibonacci sequence
c = round(GOLDEN_RATIO * c)
# if the current term is an even number, add it to 'sum'
if not(c & 1):
sum += c
# print out the sum
print(sum)And this gives out the correct sum too!
Note: It is worth noting that the level of precision for the golden ratio significantly impacts the accuracy of the obtained results. As the sequence advances, relying on the approximation of 1.618 for the golden ratio will increasingly yield inaccurate results. To avoid this, I used 10 decimal places to ensure greater accuracy.
There’s one more observation to be made. If you’ve read my last blog post, you’ll know that it never hurts to observe the sequence and see if any interesting patterns emerge from it. In this problem, we are asked to find out the sum of all even fibonacci terms under four million. Let’s highlight the even terms.
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…
Every third term in the sequence above is an even number! We can exploit this pattern to avoid checking whether a number is even or not. How? Well, if every third term in the sequence is an even number, then the next even term can be obtained by multiplying the current term with the golden ratio cubed.
i.e. current term * (golden ratio)3
Using this revelation in our code, we get the following:
# start the fibonacci seq. with 1 and 2
a = 1
b = 2
GOLDEN_RATIO = 1.6180339887
GOLDEN_RATIO_CUBED = pow(GOLDEN_RATIO, 3)
# initialize 'sum' with 0
sum = 0
# calculate the current term and store it in 'c'
c = b # here, it is 2
# run the loop as long as the current term is <= four million
while(c <= 4000000):
sum += c
# calculate the next even term of the fibonacci sequence
c = round(GOLDEN_RATIO_CUBED * c)
# print out the sum
print(sum)And yes! We get the right answer again!
Exploring unconventional approaches to problem-solving is valuable. Even though the outcomes remain the same, we continuously learn and explore new things. That’s my takeaway here!